A podcast listener asks:
It is my understanding that financial theory proposes that asset prices revert to their long-term mean. If so, does this conjecture apply to interest rates too?
Mean reversion is probably one of the most misunderstood concepts in all of finance.
On the one hand, it’s misunderstood by performance chasers who don’t take it into account by extrapolating recent performance and assuming it will continue indefinitely into the future.
On the other hand, it’s misunderstood by historically inclined investors who assume the long-term averages are written in stone and if they only wait long enough valuations or profit margins or stock prices or interest rates will surely return to those magical averages.
Scott Alexander wrote a wonderful piece at Slate Star Codex earlier this year that provides a nice example of how mean reversion works in the real world. Alexander notes there are a number of researchers who have determined through various studies using placebo drugs on sick patients that the placebo effect is likely a myth. It was most likely being mistaken for reversion to the mean:
What happened? Probably placebo effects rode on the coattails of a more important issue, regression to the mean. That is, most sick people get better eventually. This is true both for diseases like colds that naturally go away, and for diseases like depression that come in episodes which remit for a few months or years until the next relapse. People go to the doctor during times of extreme crisis, when they’re most sick. So no matter what happens, most of them will probably get better pretty quickly.
So it wasn’t necessarily that the placebos were providing a benefit; it was just that most sick people tend to get better.
This makes for a great analogy about the stock market. The stock market gets sick from time to time. Sometimes the illness is more severe than other times but it does tend to get better over time. That ebb and flow between getting sick and getting better is a good illustration of how regression to the mean works.
The hard part about regression to the mean is that:
- it doesn’t operate on a set schedule
- you could be waiting a long time to see past average levels
- historical averages can become stale once more data becomes available or as market participants adapt to new circumstances
- the averages tend to be a moving target over time
Reversion to the mean can be difficult to predict in the stock market but it’s likely even more difficult when trying to figure out the “natural” interest rate. Here’s a chart of the 10-year treasury yield going back to the start of the last century along with an updated average along the way:
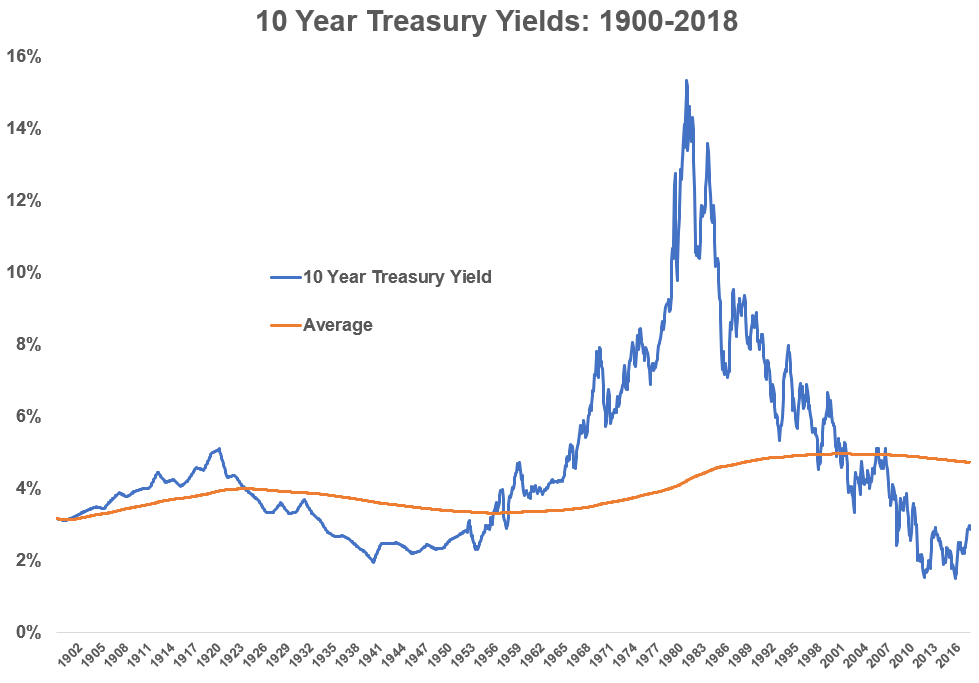
You can see that the average itself fluctuates over time. Figuring out the correct average to use in any mean reversion analysis with interest rates is made even more difficult by all of the other variables you must consider.
This chart uses nominal rates but what if we looked at real rates after inflation?
I took this data back to 1900 but inflation was more or less nonexistent until the 1940s. In fact, total inflation from 1871-1939 was around 13% (or just 0.2% per year). From 1940 through today it’s been well over 1600% (or around 3.8% per year).
You also have to take into account how mature the economy is when considering the historical track record of interest rates. William Bernstein touched on this idea in his book The Birth of Plenty:
Interest rates, according to economic historian Richard Sylla, accurately reflect a society’s health. In effect, a plot of interest rates over time is a nation’s “fever curve.” In uncertain times rates rise because there is less sense of public security and trust. Over the broad sweep of history, all of the major ancient civilizations demonstrated a “U-shaped” pattern of interest rates. There were high rates early in their history, following by slowly falling rates as the civilizations matured and stabilized. This led to low rates at the height of their development, and, finally, as the civilizations decayed, there was a return of rising rates.
So a lot of it comes down to trust in the system.
Once you boil it down there are more considerations to this analysis than first meets the eye. Here are a few more considerations when thinking about mean reversion:
Expectations matter. It’s not only the numbers themselves that matter when thinking about mean reversion but also what’s priced into the markets and what investors expect to happen that have an impact. Quantifying these variables can be extremely difficult.
High growth doesn’t last forever. The way I like to think about mean reversion when it comes to market performance is the fact that periods of above-average performance will eventually be followed by periods of below average performance. The toughest part of this equation is of course when that ‘eventually’ kicks in. The timing of these things can get you if you don’t have an open mind. Just ask all of the people waiting for profit margins and valuations to come back to their long-term averages since 2010.
Probabilities. History is never perfect when thinking about mean reversion but it can help you think probabilistically by giving you some baseline assumptions. It allows you to think in terms of a range of outcomes. Probabilistic thinking also helps you avoid the allure of certainty.
Model in overreactions. When figuring out your reasonable range of outcomes it’s helpful to remember that we humans nearly always take things too far. This leads to overreactions when things are going good and when they’re going bad.
Trees don’t grow to the sky but it’s nearly impossible to know when they’re going to be cut in half because human nature is the wild card in the timing of these things.
Tune into the podcast on Wednesday where Michael and I will be discussing this topic in further detail. And feel free to subscribe so you never miss an episode.
Further Reading:
A Short History of Interest Rates
